

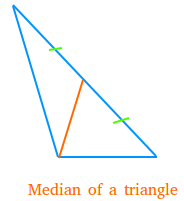
The altitude of a triangle is the perpendicular line drawn from a vertex of the triangle to the opposite side.In an equilateral triangle, the median is the same as the altitude.Areas of the number of smaller portions that a median creates within a triangle would be always equal.If three medians are drawn at a time, they will surely meet at a point of the triangle.( Centroid ).The number of medians in a triangle would be always equal to the number of vertices in the triangle.The area of the two parts formed by drawing a median (which would be two triangles) would always be equal.An altitude begins from the vertex of a triangle and ends at the point of the opposite side which divides the opposite side equally.There are some properties of a median that may be defined as its characteristics. In an equilateral triangle, the altitude is the same as the median.Altitude is a basic component that helps to calculate the area of a triangle.Altitude is a part of a triangle that always needn’t be within the sides of a triangle.If all the altitudes of a triangle are drawn at a time, then the three altitudes will surely intersect at a point called the orthocentre.The angle that an altitude makes with the opposite side would always be 90 degrees.In other words, the number of sides in a triangle would be equal to the number of altitudes. Like the median, there would be 3 altitudes in a triangle.The properties can be different for different kinds of triangles, but there are some features or key properties that make them identifiable. The altitude and median of a triangle have different properties as a part of the triangle. Where, a, b and c are sides of the triangle and ‘a’ is the side to which the median is drawn. With the help of the length of sides, we can find the length of a median, using the below formula: Similarly, all the three medians divide the sides into equal halves. In the above figure, AR is a line segment that divides side BC into two halves, that is, BR and RC. ^ Leung, Kam-tim and Suen, Suk-nam "Vectors, matrices and geometry", Hong Kong University Press, 1994, pp.The median of a triangle is a line segment drawn from a vertex to another point on the opposite side of that vertex so that the line segment divides the opposite side into two halves.^ Benyi, Arpad, "A Heron-type formula for the triangle", Mathematical Gazette 87, July 2003, 324–326.^ Boskoff, Homentcovschi, and Suceava (2009), Mathematical Gazette, Note 93.15.^ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp.^ Sallows, Lee, " A Triangle Theorem Archived at the Wayback Machine" Mathematics Magazine, Vol.DOI 10.2307/3615256 Archived at the Wayback Machine E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108. "Medians and Area Bisectors of a Triangle". CRC Concise Encyclopedia of Mathematics, Second Edition. The lengths of the medians can be obtained from Apollonius' theorem as: If the two triangles in each such pair are rotated about their common midpoint until they meet so as to share a common side, then the three new triangles formed by the union of each pair are congruent. In 2014 Lee Sallows discovered the following theorem: The medians of any triangle dissect it into six equal area smaller triangles as in the figure above where three adjacent pairs of triangles meet at the midpoints D, E and F. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.) The three medians divide the triangle into six smaller triangles of equal area.Ĭonsider a triangle ABC.
The centroid is twice as close along any median to the side that the median intersects as it is to the vertex it emanates from.Įach median divides the area of the triangle in half hence the name, and hence a triangular object of uniform density would balance on any median. Thus the object would balance on the intersection point of the medians. The concept of a median extends to tetrahedra.Įach median of a triangle passes through the triangle's centroid, which is the center of mass of an infinitely thin object of uniform density coinciding with the triangle.
In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid. In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Not to be confused with Geometric median.


 0 kommentar(er)
0 kommentar(er)
